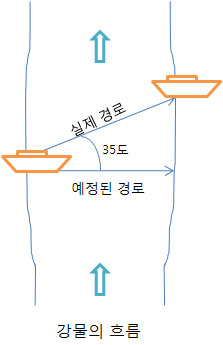
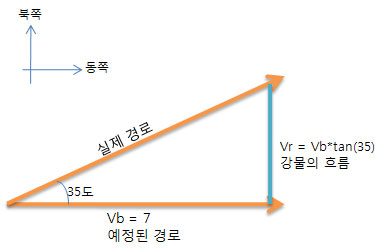
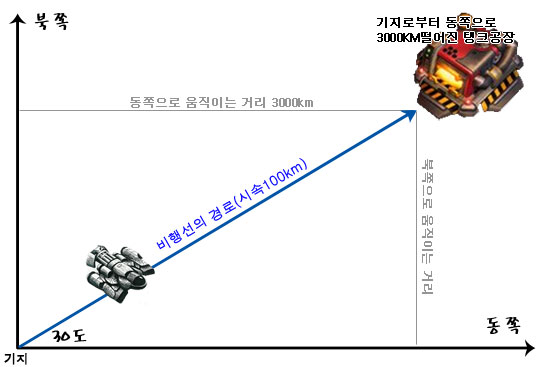
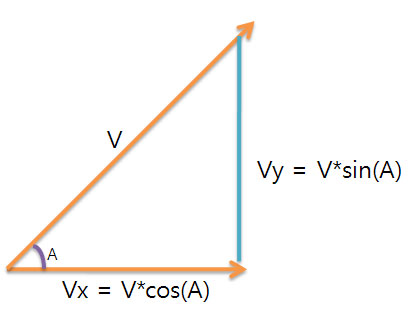
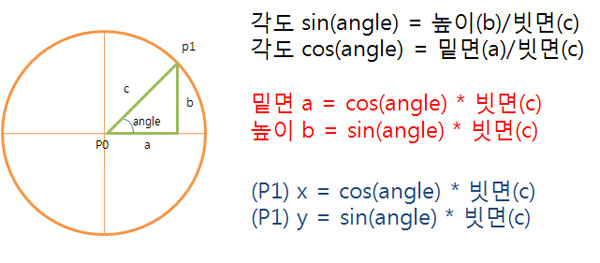
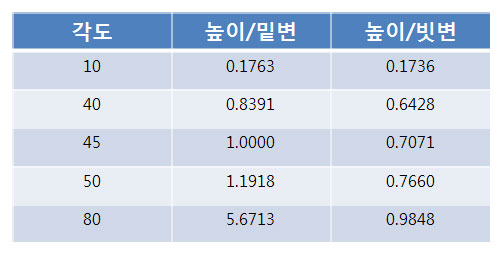
축척을 하거나 거리, 각의 크기를 할고자 할때 삼각형을 사용하여 그 값을 구한다.
각도는 흔히 알고있는 360도를 사용하며 반으로 나눈 180도를 평각의 크기로 정하였다, 또 평각의 4분의 1은 45도로 정하고 평각의 6분의 1은 30도로 하였다.
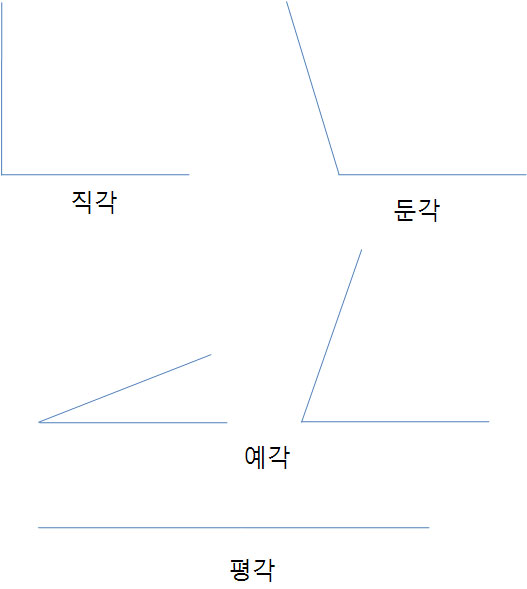
직각은 두직선이 만나는 각도의 크기가 직각 90도일 때의 각도이다.
예각은 두직선이 만나는 각도가 90도 보다 작을때의 각도이다.
둔각은 두직선이 만나는 각도가 90도 보다 클때의 각도이다.
평각은 두직선이 일직선으로 이어질때의 각도이다.이외에 여각이라는 크기가 있다.
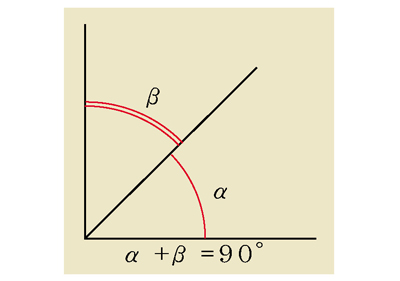
여각은 두각의 합이 90도일 때 한각의 크기를 여각이라 한다.
위의 그림에서 a(알파)의 여각은 b(베타)이고 b의 여각은 a이다.
참고) 미세한 각도는 1도보다 작은 1/60각을 분이라하고 이 분을 1/60하면 초라고한다.
어찌보면 시계의 초침과 분침을 생각하면 비슷하지만 사실 우연히 단위가 일치하게 된것일 뿐이다. 시계는 초침도 360를 회전하게 되고 분침도 360를 돌아야 분과 초의 단위가 올가지만 각도의 분과 초는 정말 작은 각도의 단위인 것이다.
1분 = 1/60도
1초 = 1/60분
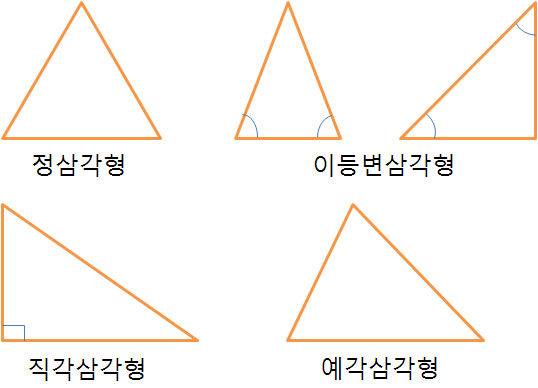
이러한 각도의 정의로 삼각형의 종류를 알수 있다.
정삼각형은 세각의 크기가 같고 세변의 크기가 같은 삼각형이다.
이등변삼각형은 두변의 크기가 같다. 이때 길이가 같은 두변이 마주보는 각도의 크기도 같다.
직각삼각형은 삼각형의 각들중 하나가 직각인 경우이다.많이 쓰이지는 않지만 예각 삼각형은 세각의 크기가 전부 90보다 작을때 불려지고 그림에는 없지만
한각의 크기가 90보다 크면 둔각삼각형이라고 한다.
이러한 삼각형에는 몇가지 특징이 있다.
삼각형의 각도의 합은 180도이다. 사각형은 삼각형2개가 모여 이룰수있으므로 360도이고 오각형은 삼각형 3개로 표현이 가능하다 따라서 540도이다.
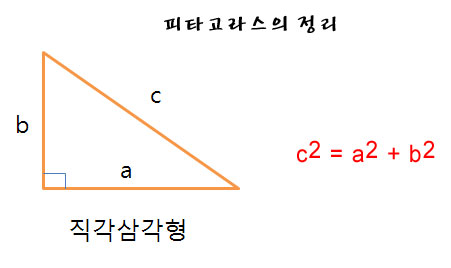
그리고 직각삼각형 일때 빗변제곱의 크기는 밑변의 제곱과 높이의 제곱을 더한 값과 같다는 피타고라스의 정리도 있다.
피타고라스의 정리는 두점의 거리를 구하거나 점의 위치를 구할 때 많이 사용된다.
흔히 척도를 하기 위해서는 비율이 일정한 삼각형을 사용한다. 가령 나무의 길이를 알고자 할 때 그림자와 태양의 각도가 45도일때 측정한 그림자의 길이를 구하여 이를 1/100 정도의 작은 크기로 단위를 내서 구한 값으로 나무의 길이를 구할 수 있다.
사물과 세상에는 엄청나게 큰 단위들이 있다 가령 서울과 부산과의 거리...어느별과 지구와의 거리등을 구하기 위해서는 다누이가 엄청 크기때문에 지수법으로 단위를 줄여 사용하기도 한다.
* 지수표기법2,340,000,000은 간단히 2.34 * 10
9 으로 표현하고 이는 다음과 같이 사용한다.
2,340,000,000 -> 3.34E9이와 같은 표기법은 지수표기법이라고 한다. 여기서 E는 지수(Exponent)를 뜻한다. E 다음에 쓰여진 숫자는 몇
승인지를 의미한다. 위의 예에서는 10에 관한 지수를 표현한 것이다.
AS3에서는
Math.pow(10 , 9)가
10에 관한 E9과 같은 표기법이 된다.