아주 예전에 직각 삼각형을 이용하여 거리를 구하거나 위치 등을 구할때 직각삼각형을 이용한 피타고라스의 정리로 구하기 힘든 거리를 구하였는데 건축과 생활의 거리, 높이 등을 각도에 의하여 도표를 만들어 보았는데 그 비율은 항상 같은 각을 갖는 직각삼각형에는 크기는 달라도 모두 같은 면의 길이 비율의 값을 갖는 것을 발견하였다.
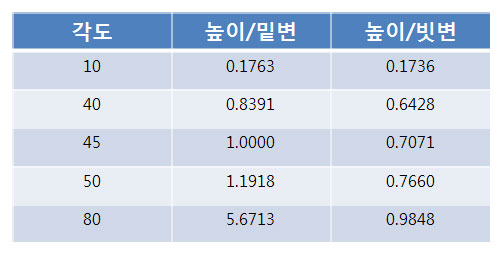

[위의 비율은 삼각형의 크기와 상관없이 같은 각이면 비율이 같았다]
우선 이러한 비율에 이름을 정의하였는데
각을 θ각이라고 할때 높이/밑변 = 함수 f(θ)이다. 이 함수의 이름을 탄젠트(go off on tangent : 작명중 대화의 주제에서 벗었났다 에서 유래되었다는 설도 있고 가장 유력한 것은 탄젠트는 접촉하고 있다는 의미를 가진 라틴어 tangens에서 온겁입니다. 이러한 이유로 tangent가 접선으로 번역되고 있기도 하구요..
탄젠트라는 용어는 덴마크의 수학자 핑케가 만든것으로 알려져 있습니다)라 지었다.
tan(θ) = 높이/밑변의 비율
마찬가지로 높이/빗변 = 함수 f(θ)에 따라 일정하므로 이름을 사인(1624년 영국의 수학자 군터가
처음으로 사용하였답니다. sine은 길의 커브, 땅의 움푹들어간 곳, 꼬불꼬불한 길, 옷의 주름, 주머니, 만(灣), 가슴등의 뜻을 가진 라틴어 sinus에서 온것이라 합니다.)이라고 지었다.
sin(θ) = 높이/빗변의 비율
마지막으로 밑변/빗변= 함수 f()에 따라 일정한 비율을 갖는 코사이(cosine이란 말은 complementary sine을 줄인 것으로 여각의 사인이란 의미를 가집니다.cosine도 역시 라틴어 cosinus에서 온 것으로, 1620년 군터가 complementum sinus를 합친 co.sinus를 제안했었고 1658년에 뉴턴에 의해 cosinus로 수정되었습니다. 그후, cos이란 기호는 1729년 오일러가 사용하였답니다.)이 정의 되었습니다.
cos(θ) = 밑변/빗변의 비율
* 직각삼각형의 성질상 빗변은 밑변이나 높이보다 적을수가 없습니다. 따라서 sin과 cos의 비율은 각도의 크기와는 상관없이 항상1보다 작은 무리수(대부분의 삼각함수의 값)로 나타납니다.
이처럼 삼각법의 비율을 가지고 세변중 두개의 길이를 알면 각도를 구할 수 있고 각도와 한 변의 길이를 알면 밑변(x)와 높이(y) , 빗변을 구할수 있게 된다. 이러한 좌표계가 직각좌표계이다. 나중에 다루어 보겠지만 이러한 좌표계말고도 원점을 정하고 특정좌표를 구하기위에 반지름과 θ만을 사용하여 구하는 극좌표계가 있다.


