속도는 어떠한 물체가 어떠한 속력(힘)으로 움직이는 운동상태에 방향(변위)가 추가된 것이다. (참고 : 속도와가속도) 속도를 알기 위한 성분으로는 동서남북과 같은 또는 x축 y축과 같은 이동하는 방향에 따른 기준이 될 수 있는 속도벡터를 가지고 계산할 수 있다.
* 속도벡터 : 운동하고 있는 물체의 각 시점에서의 순간 속도에 비례하는 길이를 갖고, 운동하는 방향과 나란하게 그은 벡터.
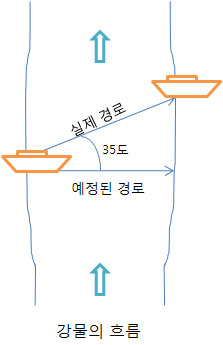
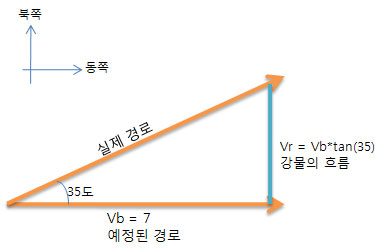
가령 북쪽으로 시속10키로로 향하고 동쪽으로 시속 10키로로 이동하는 물체가 있다고 할 때 북쪽으로 이동하는 성분과 동쪽으로 이동하는 성분의 크기를 가지고 북동쪽으로 이동하는 선을 속도벡터라고 하고 시간과 거리를 삼각법으로 구할 수 있다.
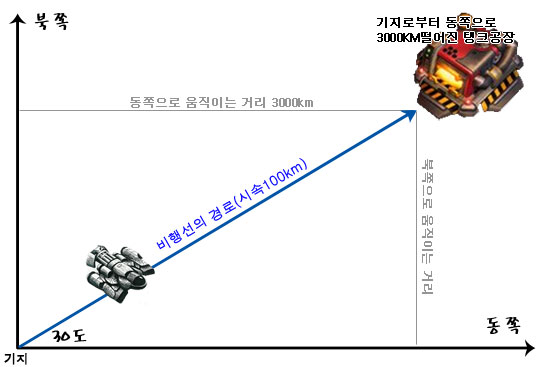
기지에서 드랍쉽이 출발하여 공장에 탱크들을 태우러 가야한다. 탱크공장은 기지에서 동쪽으로 3000키로미터 떨어져 있고 지도상의 각도는 북쪽으로 30도 에 있을때 비행선이 공장으로 시속 100km씩 직선 이동하면 몇 시간후에 도착할까?
이 값을 구하기 위한 값은 거의 다 나와있는 것 같다. 기지로부터 공장까지의 직선 각도는 30도이고 공장의 위치는 직각좌표계로 보자면 x = 3000인 셈이다. 따라서 밑변의 값과 각도를 알고 있음므로 cos에 관하여 식을 세워보면,
cos(30) = 시간당 동쪽벡터/빗변(시간당 이동거리)의 비율이므로 현재 이동할 총 거리는 몰라도 시속 100km를 대입하여
한시간 동안의 이동 거리를 정리하면
동쪽으로 1시간 동안 이동하는 거리 = cos(30) * 100km 이고 cos(30)은 0.8660이다. 따라서 동쪽으로 비행선은 시속 86.6km씩 움직이고,
(동쪽 총 거리 3000) / (시간당 움직이는 동쪽거리86.6) 으로 하면
34.64시간 후에 공장에 도달하게 된다...사실 이렇게 늦게 도착하면 게임에서 지겠네요...
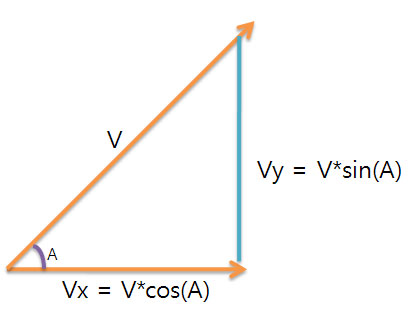
* 속도성분일단 두 방향을 정하고 각각을 x방향 , y방향이라고 한다.(에를 들어 위의 경우처럼 x는 동쪽 , y는 북쪽으로 정하고 두방향은 반드시 직각이여야 한다.) 그리고 v가 아무 방향의 속도라고할 때 x성분과 y성분은 각각 다음의 공식으로 계산 할 수 있다.
Vx = V * cos(각도)
Vy = V * sin(각도)
[ 속도성분 계산식 ]